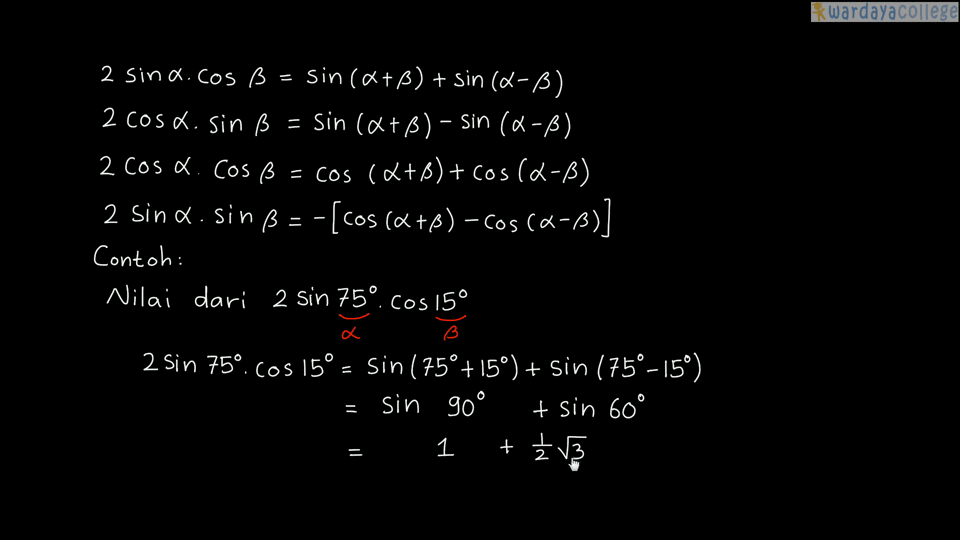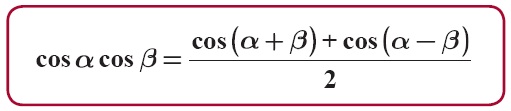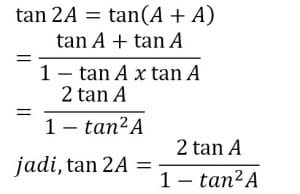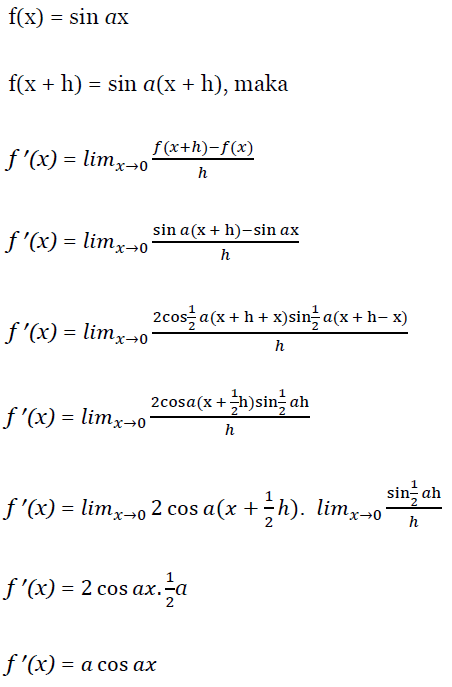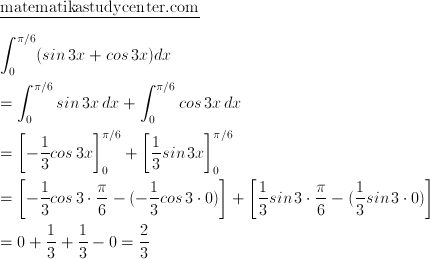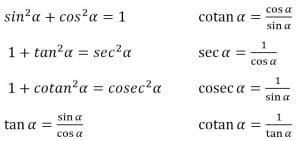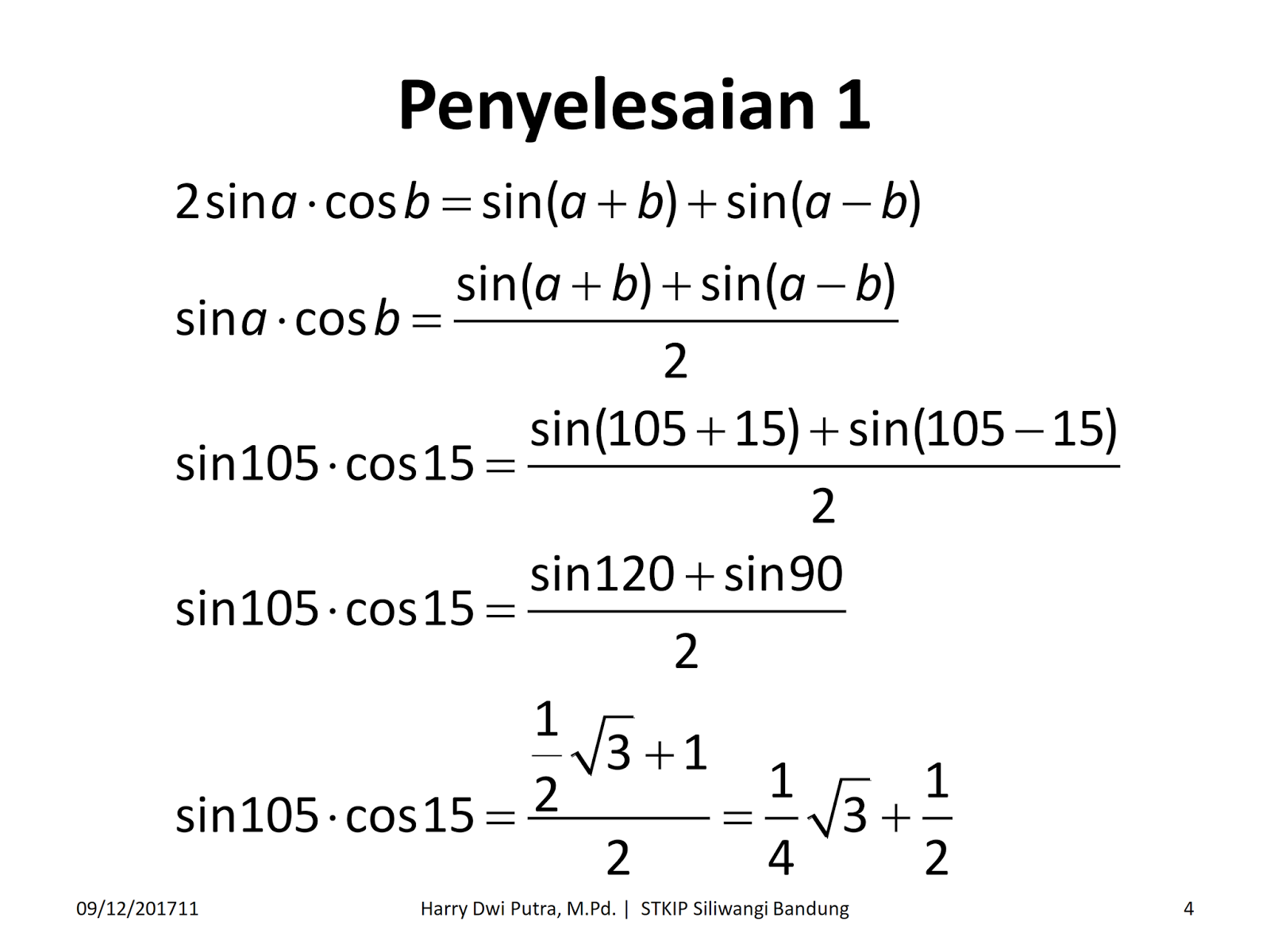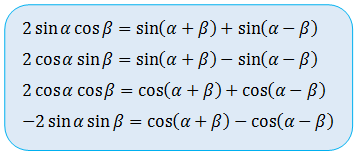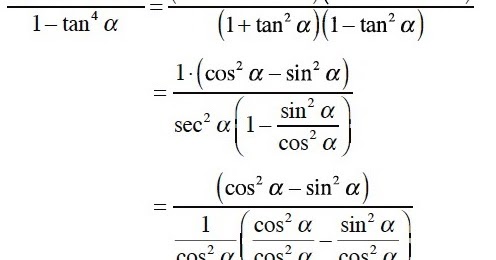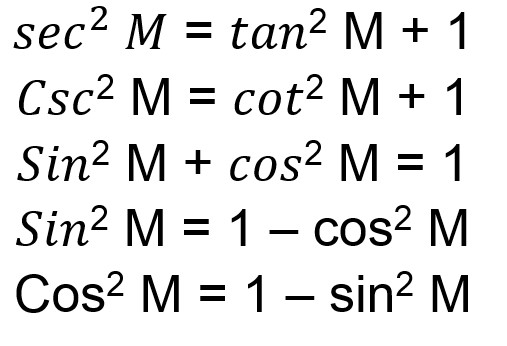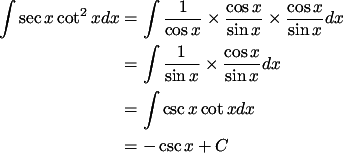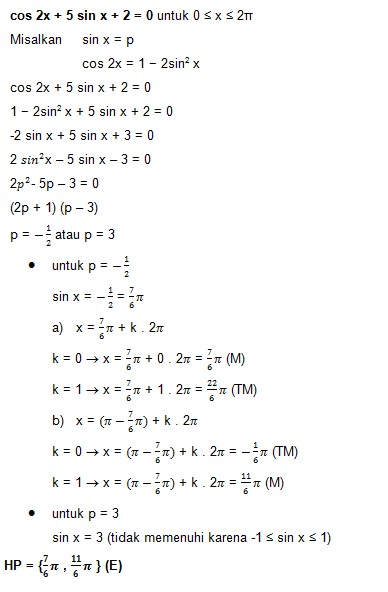Perkalian Trigonometri
Rumus Trigonometri Dan Fungsi Trigonometri Matematika
rumusrumus.com
Contoh Soal Tentang Penjumlahan Dan Pengurangan Trigonometri Ilmu Hitung
ilmuhitung.com
Perkalian Trigonometri Pdf Document
fdokumen.site
Page 10 Trigonometri
ummpress.umm.ac.id
Soal Dan Pembahasan Super Lengkap Penerapan Identitas Trigonometri Mathcyber1997
mathcyber1997.com
Pembuktian Rumus Perkalian Trigonometri Dan Contoh Soal Edumatik Net
edumatik.net
Selanjutnya perhatikan pengurangan antara rumus jumlah dan selisih dua sudut fungsi sinus.
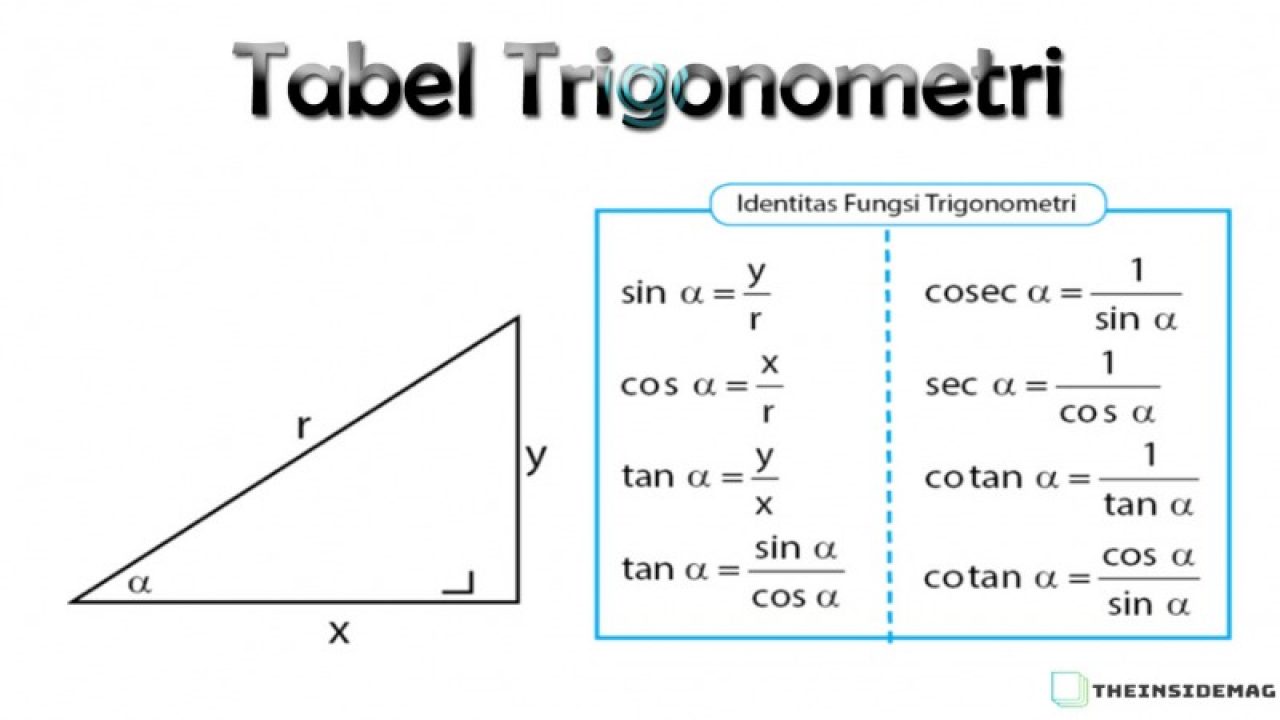
Perkalian trigonometri. Jika belum tahu atau belum hafal bisa lihat dulu di sini. Identitas trigonometri merupakan salah satu sub pokok bahasan trigonometri. Blog koma materi rumus perkalian penjumlahan dan pengurangan trigonometri merupakan kelanjutan dari materi rumus trigonometri untuk jumlah dan selisih dua sudutsilahkan juga baca materi perbandingan trigonometri sudut sudut berelasirumus perkalian penjumlahan dan pengurangan trigonometri ini biasanya akan banyak kita gunakan pada materi integral dan limit.
Untuk menyelesaikan persamaan trigonometri pada kalimat terbuka dan itu artinya menentukan nilai variabel yang ada pada persamaan tersebut. Khususnya dalam pembahasan ini saya hanya fokus dengan pembahasan soal soal. Pembuktian rumus perkalian fungsi sinus dan cosinus dapat menggunakan rumus rumus jumlah dan selisih dua sudut pada fungsi trigonometri.
Pembuktian rumus perkalian trigonometri dan contoh soal. Selain itu kita juga akan membahas contoh soal rumus perkalian sinus dan cosinus akan tetapi sebelum membahas materi ini sebaiknya kamu membaca dulu matari sebelumnya yaitu rumus jumlah dan selisih dua sudut sebab pembuktian rumus pada materi ini berawal dari materi tersebut. Persamaan trigonometri ini juga terbagi di dalam dua bentuk antara lain yaitu berbentuk kalimat terbuka dan juga berbentuk identitas.
Bisa dibilang gampang saat kita mengerti dan paham dengan semua identitas trigonometri. Rumus rumus penjumlahan pengurangan atau perkalian dalam trigonometri dapat diturunkan dari rumus jumlah dua sudut atau selisih dua sudut. Tangent cosecan secan dan cotangent bisa digunakan bersama sama baik dengan penjumlahan atau pengurangan maupun perkalian.
Dan akan menjadi hal tersulit dalam pelajaran matematika jika kita sama sekali belum paham tentang perkalian trigonometri.
Rumus Trigonometri Penjumlahan Pengurangan Perkalian Segitiga
www.studiobelajar.com
Perkalian Trigonometri
www.slideshare.net
Rumus Sudut Rangkap Trigonometri Dan Contoh Soalnya Lengkap
rumusbilangan.com
Pelajaran Soal Rumus Perkalian Fungsi Trigonometri Wardaya College
www.wardayacollege.com
Materi Lengkap Trigonometri Dengan Fungsi Rumus Dan Pembahasan Contoh Soal
www.utakatikotak.com
Teknik Integral Substitusi Fungsi Trigonometri
maths.id
Rumus Rumus Trigonometri Rumus Perkalian Sinus Dan Kosinus Jibang Pardamean Hutagaol Berbagi Ilmu Matematika Informasi
www.ruangparabintang.com
Rumus Integral Trigonometri Rumushitung Com
rumushitung.com
Kalkulus Sifat Trigonometri Mahendra Bayu Wardhana
mahendrabayuwardhana.wordpress.com
Trigonometri Pengertian Identitas Fungsi Rumus Dan Contoh
4winmobile.com
1 Nyatakan 2 Cos 75 Cos 15 Ke Dalam Bentuk Jumlah Atau Selisih Kemudian Tentukan Hasilnya 2 Brainly Co Id
brainly.co.id
Rumus Perkalian Sinus Dan Cosinus Penjumlahan Pengurangan Contoh Soal Jawaban Jumlah Selisih Trigonometri Matematika
www.nafiun.com
Materi Lengkap Trigonometri Dengan Fungsi Rumus Dan Pembahasan Contoh Soal Pelajaran Sekolah Online
www.pelajaran.co.id
Penjumlahan Dan Perkalian Trigonometri
id.scribd.com
Trigonometri Sutrisno Ppt Download
slideplayer.info
Unacademy India S Largest Learning Platform
unacademy.com
3
encrypted-tbn0.gstatic.com
Perkalian Trigonometri
www.slideshare.net
1
encrypted-tbn0.gstatic.com
Rumus Perkalian Fungsi Trigonometri Sinus Dan Cosinus Idschool
idschool.net
Contoh Soal Perkalian Sinus Dan Cosinus Dan Pembahasan Soalfismat Com
soalfismat.com
Rpp Tps Rumus Perkalian Sinus Kosinus Badrulaini 3no076xo9end
idoc.pub
Perkalian Trigonometri
www.slideshare.net
Rumus Penjumlahan Dan Pengurangan Trigonometri Dan Contoh Soal Marthamatika
www.marthamatika.com
Rumus Penjumlahan Dan Pengurangan Fungsi Sin Dan Cos Idschool
idschool.net
Limit Trigonometri Rumushitung Com
rumushitung.com
Perkalian Dan Penjumlahan Sinus Dan Kosinus Harry Dp
www.harrydp.ml
Pengertian Trigonometri Fungsi Rumus Dan Contoh Soal Rumuspelajaran Com
www.rumuspelajaran.com
Cara Mengerjakan Turunan Fungsi Trigonometri
mafia.mafiaol.com
Trigonometri Wikipedia Bahasa Indonesia Ensiklopedia Bebas
id.wikipedia.org
Identitas Trigonometri
statmat.id
Soal Integral Trigonometri Perkalian Cosinus Kelas Xii Ipa
istanamatematika.com
Integral Trigonometri Rumus Integral Cos Soal Pembahasan
www.dosenpendidikan.co.id
Limit Trigonometri Penjelasan Soal Soal Limit Trigonometri
rumusguru.com
Inilah Kumpulan Rumus Trigonometri Dalam Matematika
paluipuntik.com
Integral Trigonometri Un Matematika Sma
matematikastudycenter.com
Limit Trigonometri Pengertian Rumus Identitas Fungsi Contoh Soal
rumus.co.id
Perkalian Trigonometri Toffeedev International Flickr
www.flickr.com
Pengertian Trigonometri Dan Rumus Trigonometri Lengkap Dengan Soal
www.utakatikotak.com
Contoh Soal Trigonometri Jumlah Selisih Dua Sudut Sains Seru
www.sainsseru.com
Pembuktian Rumus Penjumlahan Trigonometri Dan Contoh Soal Edumatik Net
edumatik.net
T0kivitlaa0hem
Rumus Penjumlahan Pengurangan Dan Perkalian Trigonometri Mathsteria
mathsteria.wordpress.com
Rumus Trigonometri Dan Contoh Contoh Soal Beserta Jawabannya
www.pinterpandai.com
Rumus Trigonometri Ulasan Dan Berbagai Contoh Soalnya Kelas Pintar
www.kelaspintar.id
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcqnzzrkxcjvr9dcuvnjl9gom5u9mulwymroqyu6wzyxbenvnavq Usqp Cau
encrypted-tbn0.gstatic.com
Belajar Matematika Online Rumus Rumus Trigonometri
soulmath4u.blogspot.com
Trigonometri Mathematics Quiz Quizizz
quizizz.com
Rumus Perkalian Sin Cos Cara Menghapal Youtube
www.youtube.com
Rumus Jumlah Dan Selisih Fungsi Trigonometri Sinus Dan Cosinus
maths.id
Rumus Trigonometri Serta Cara Memperolehnya Rumus Matematika
rumus-matematika.com
Rumus Trigonometri Ulasan Dan Berbagai Contoh Soalnya Kelas Pintar
www.kelaspintar.id
Rumus Perkalian Sinus Dan Cosinus Lengkap Beserta Contohnya
www.sheetmath.com
Trigonometri Rumus Perkalian Sinus Dan Kosinus Tri Khidayanti
www.trikhidayanti.web.id
Perkalian Pada Trigonometri Sman 15 Surabaya
sman15-sby.sch.id
Pemahaman Rumus Perkalian Trigonometri Showme
www.showme.com
Do The Best Rumus Rumus Trigonometri
sisil07.blogspot.com
Perkalian Dan Penjumlahan Sinus Dan Kosinus Harry Dp
www.harrydp.ml
Pembuktian Rumus Perkalian Trigonometri Dan Contoh Soal Edumatik Net
edumatik.net
04 Bab 3
www.yumpu.com
Contoh Soal Dan Pembahasan Jumlah Dan Selisih Sinus Dan Cosinus Guru Ilmu Sosial
www.ilmusosial.id
Rangkuman Contoh Soal Pembahasan Trigonometri
tanya-tanya.com
Contoh Soal Dan Pembahasan Trigonometri Kelas Xi Guru Ilmu Sosial
www.ilmusosial.id
Perkalian Silang Dua Vektor Konsep Matematika Koma
www.konsep-matematika.com
Identitas Trigonometri Ppt Download
slideplayer.info
Un Sma 2017 Matematika Ipa Pembahasan No 25 Rumus Perkalian Trigonometri Youtube
www.youtube.com
Integral Trigonometri Pendidikan Matematika
yos3prens.wordpress.com
Rumus Perkalian Trigonometri Sinus Dan Cosinus Sains Seru
www.sainsseru.com
Trigonometri Bagian 2 Tutorial Matematika Kesekolah Com
www.kesekolah.com
Identitas Trigonometri Lengkap Pengertian Rumus Contoh Soal
rumus.co.id
Rumus Perkalian Sinus Dan Cosinus Serta Contohnya
www.mahirmatematika.com
Contoh Soal Pembuktian Identitas Perkalian Trigonometri Ilmu Hitung
ilmuhitung.com
Rumus Trigonometri Ulasan Dan Berbagai Contoh Soalnya Kelas Pintar
www.kelaspintar.id
Trigonometri Identitas Rumus Turunan Tabel Contoh Soal
www.yuksinau.id
Solusi Super Menyelesaikan Limit Fungsi Trigonometri Buat Anak Kelas 11
www.quipper.com
Rumus Penjumlahan Dan Perkalian Trigonometri
www.edutafsi.com
Rumus Perkalian Penjumlahan Dan Pengurangan Trigonometri Konsep Matematika Koma
www.konsep-matematika.com
Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcrstkueymatnhp1hozgdcewpg9t2oyp2cwfqzu Po E06osistr Usqp Cau
encrypted-tbn0.gstatic.com
Perkalian Trigonometri
www.slideshare.net
Kumpulan Rumus Trigonometri Contoh Soal Jawaban Lengkap
ayoksinau.teknosentrik.com
Integral Trigonometri Un Matematika Sma
matematikastudycenter.com
Rumus Trigonometri Belajar Matematika Dengan Mudah
informazone.com
Doc Kumpulan Rumus Trigonometri Kelas Xi Sma Fikri Nurham Academia Edu
www.academia.edu
Rumus Trigonometri Dasar Cos Sinus Tangen Dan Contoh Soal
majalahpendidikan.com
Soal Integral Fungsi Trigonometri
maths.id
Turunan Trigonometri Matematika Kelas 11 Quipper Blog
www.quipper.com
Contoh Soal Persamaan Trigonometri Pilihan Ganda Pembahasan
soalkimia.com
Rumus Trigonometri Untuk Perkalian Sinus Dan Kosinus
id.scribd.com
Cara Mudah Menghafal Rumus Trigonometri Identitas Jumlah Dan Selisih Perkalian Lengkap Sekolah Matematika Sains Sms
sekolah-matematika-sains.blogspot.com
Trigonometri Rumus Turunan Tabel Dan Contoh Soal Trigonometri
www.pintarnesia.com
Rumus Perkalian Trigonometri Dan Contoh Soal Marthamatika
www.marthamatika.com
Trigonometri Pembuktian Perkalian Sinus Dan Cosinus Youtube
m.youtube.com
Belajar Matematika Mudah Dan Menyenangkan Trik Menghafal Perkalian Dan Penjumlahan Bentuk Trigonometri
pak-saiful.blogspot.com
Tabel Trigonometri
tengahviral.com
May Hastuti Lubis Blog Archive Rumus Trigonometri Matematika Sma Kelas Xi
berita.student.umm.ac.id
Rumus Trigonometri Sudut Rangkap
www.mahirmatematika.com
Matematika Ssc Trigonometri Perkalian Dan Penjumlahan
matematikassc.blogspot.com
Kumpulan Rumus Trigonometri Sd Smp Sma Paling Lengkap
www.tomatalikuang.com
